Greedy的題目我認為是最難寫的，原因是我們如果沒有經過證明，會很難知道這是可行的答案，不過這邊還是找了幾題想讓大家感受一下Greedy演算法的思想。
另外，撇除掉寫題目，在日常用途上Greedy真正的用途在於能夠先給我們一個「近似解」而不是「正解」，這樣能夠至少讓我們的問題有一個合理的答案。

範例1-Maximum Units on a Truck

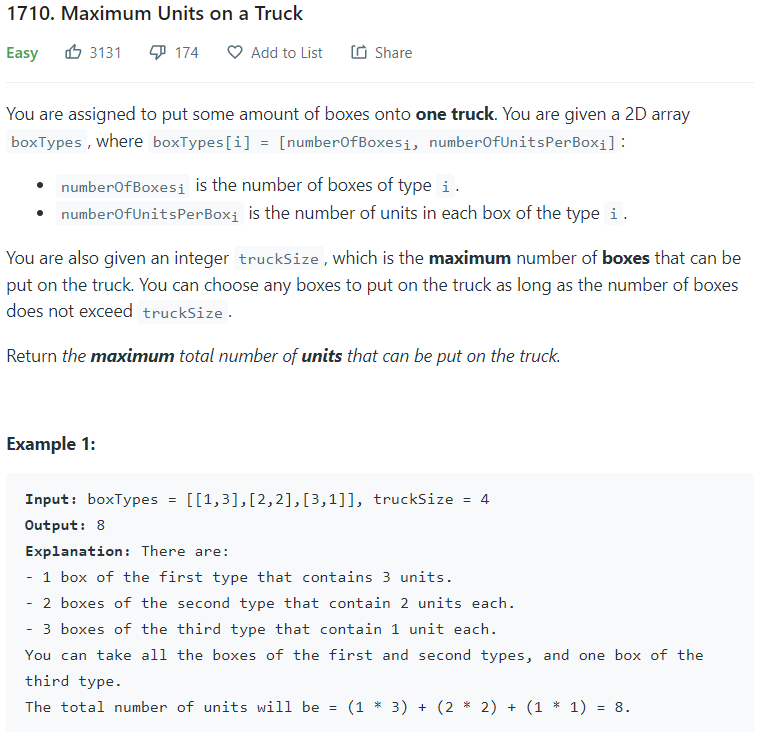
這一題題目有一點長，我在這邊也稍微用中文解釋一下，題目給我們一個boxTypes的Array以及truckSize，boxTypes[i][0]代表著第i種箱子共有幾個，boxTypes[i][1]代表這種箱子能夠裝幾個單位的東西，truckSize代表最多我可以載多少個箱子，要問我總共最多可以載走多少「單位」的東西。

這邊可以發現，這個問題就好像我們在介紹Greedy的時候提到買玩具的問題，我要最大化我的結果，我要從可以裝最多單位的箱子開始選！如果這類的箱子選完而我的貨車還有空位的話，我就選可以裝第二多的箱子，一直到我把貨車塞滿囉！
所以我們可以先依照第Array Item裡的二個key也就是「可以裝的單位數」來從大到小排序，然後依次放入貨車，這樣這題就完成拉！

class Solution:
    def maximumUnits(self, boxTypes: List[List[int]], truckSize: int) -> int:
        
        boxTypes = sorted(boxTypes, key=lambda x: x[1], reverse= True)
        res = 0
        for box_type in boxTypes:
            if truckSize == 0:
                return res
            if box_type[0] > truckSize:
                res += box_type[1]*truckSize
                return res
            res += box_type[1] * box_type[0]
            truckSize -= box_type[0]
        return res

範例2-Jump Game

選擇的思維

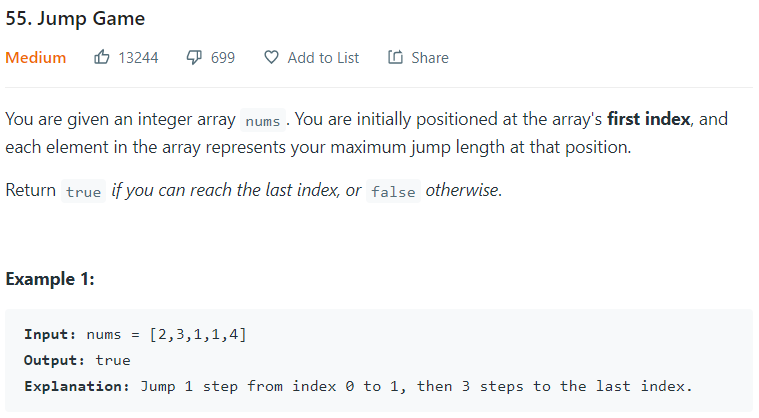
接著我們先來看看這一題，一開始我會建議讀者們用最直觀的方法來思考。一開始我們站在index 0的位子，我們最多可以跳幾步？我們可以跳2步，意思就是說目前為止「最遠」我可以到index是2的位置，我當然也可以選擇跳到index是1的位子。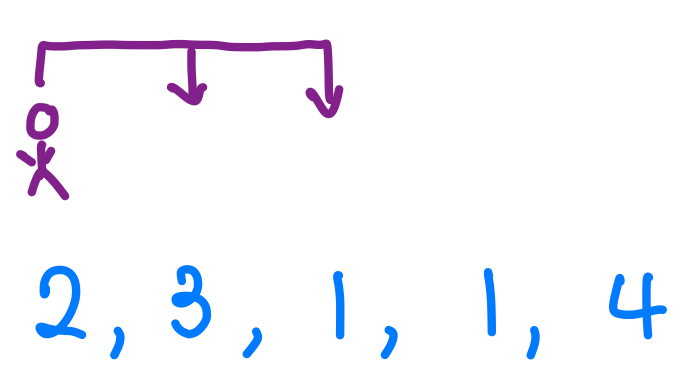

那我應該選擇跳到哪裡呢？這邊我們可能會想，我就跳到數字最大的那裏，這樣下一次跳會比較遠，但是這樣想會有一個問題，如果數字大的index比較小那怎麼辦呢？這種情況如果我跳到index 1也就是3的位置，我是沒辦法跳到最後的。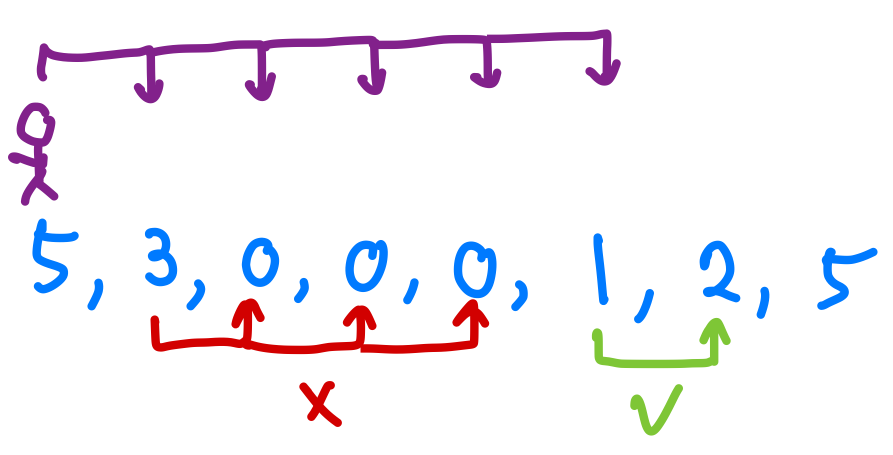

這題如果用這種思想去解其實也是可以的，但是會相對複雜一點，今天就讓我用另一種思想來解這題吧！

另外一種思維

我們來轉換我們的思維，變成「在這個位置，我最遠能跳到哪裡？」，如果我把最後一跳跳完，還沒辦法到終點，那就回傳False，否則回傳True。
我現在在index 0的位置，我可以跳兩步，所以代表說我第1步最多可以跳到index 2的地方，那我在index 2的地方做一個記號代表我現在「最遠」可以到index 2的位置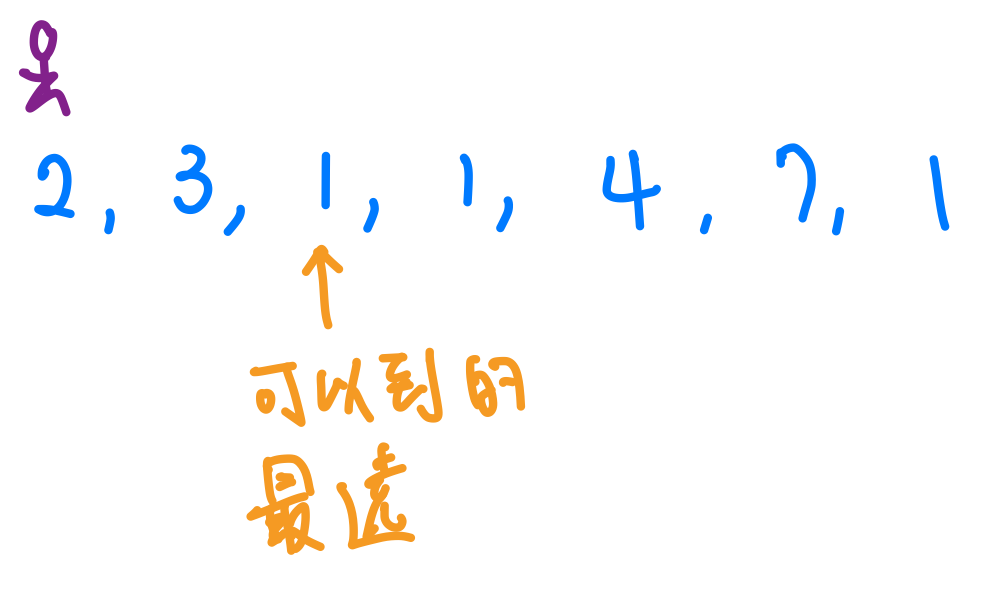

接著我把指針從index 0挪到index 1看看如果我從index 1跳最遠可以跳到哪裡？我們不用擔心能不能夠跳到index 1的位置，因為我們目前已經確認過，最遠可以跳到index 2的位置，所以index 1是一定到的了的。而且說不定我們從index 1可以跳到更遠的位置。接著我在看從index 1的位置最遠可以跳到哪裡，答案是4，現在我們可以說，最遠可以到達4的位置了。
接著我們在把指針挪到index2的位置，一樣計算如果我從index 2跳，最遠可以跳到哪裡？答案是3，這個3並沒有比4大，所以我們不用刻意去更新遠的指標，一直持續這樣我們就可以得到答案了。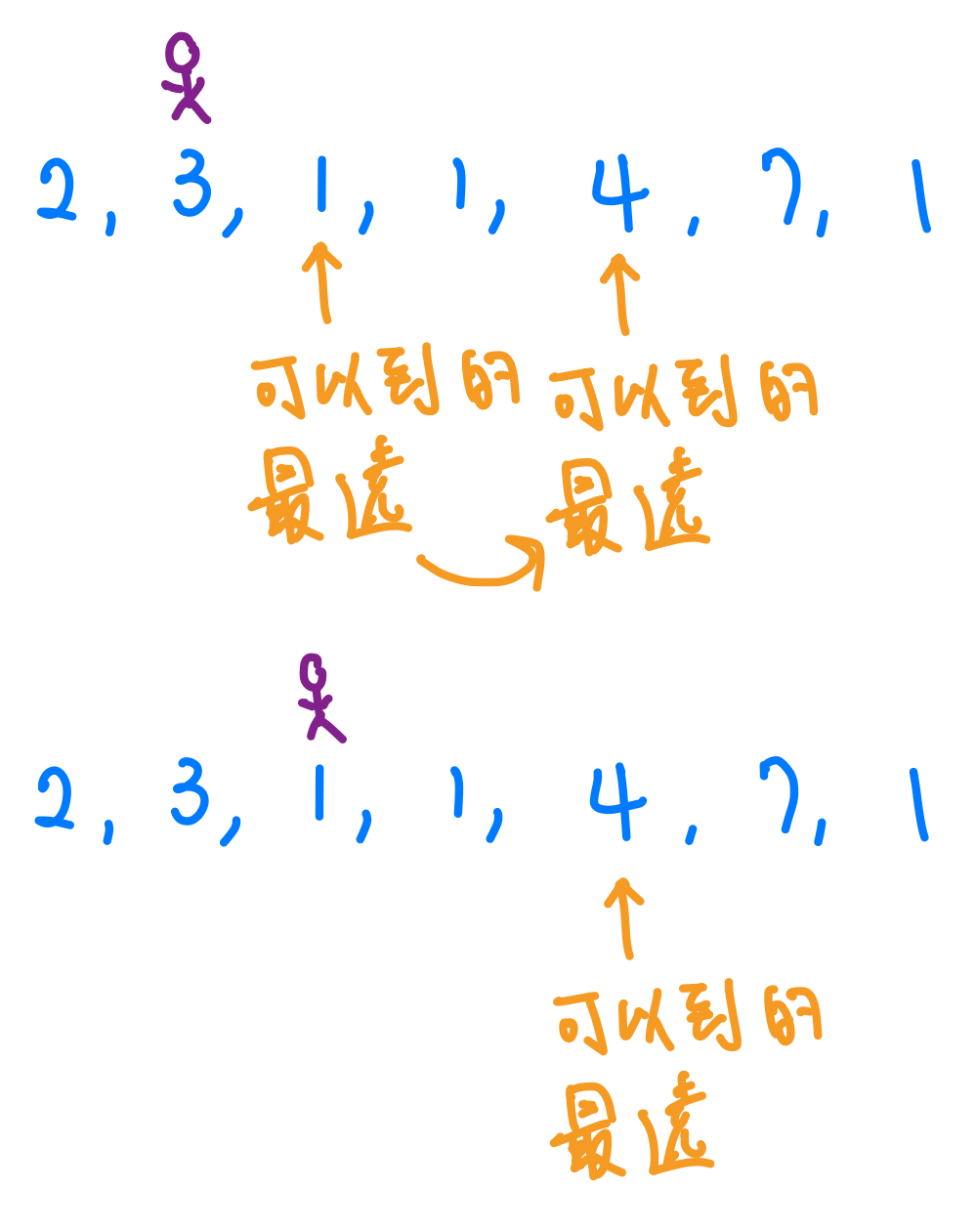

這樣持續下去的時候有一種情況代表我們跳的到終點，就是當我最遠可以到的指標大於或等於我最後的index。

相反的，如果我站在的位置，大於我可以到的最遠距離，那就可以回傳False囉！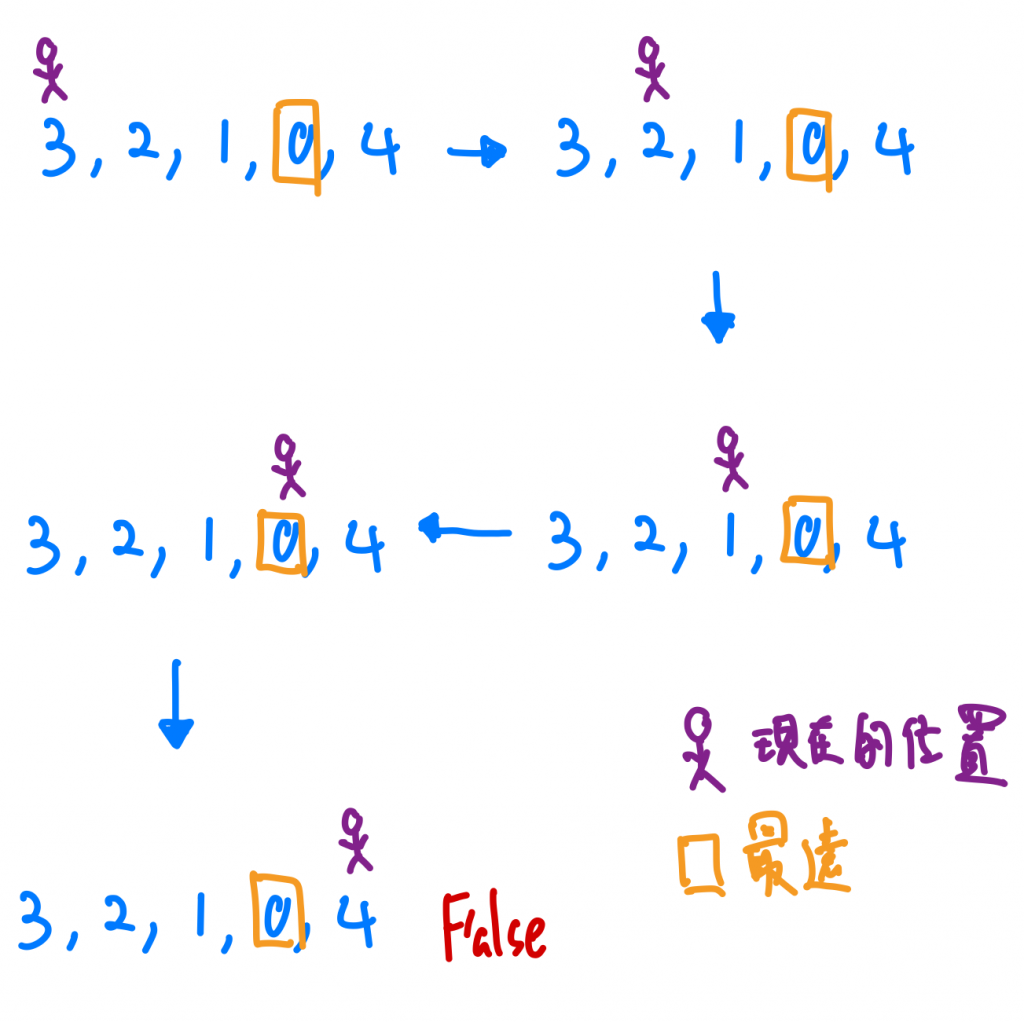

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        
        reachable = 0
        for i in range(len(nums)-1):
            if i > reachable: return False
            reachable = max(reachable, i + nums[i])
        if reachable >= len(nums)-1: return True
        else: return False